使用马拉车算法解决最长回文子串问题

发表于 2020-01-05 分类于技术，数据结构与算法

使用马拉车算法（即 Manacher's Algorithm）可以将解决最长回文子串（即 Longest Palindromic Substring）问题的时间复杂度降至 O(n)。

1 最长回文子串问题

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

2 马拉车算法

2.1 添加字符 `#` 用以解决回文子串中的奇偶性问题

添加字符 #，使得字符串 s 中每个字符的左右两侧都有一个 #，比如：

bob  -> #b#o#b#
noon -> #n#o#o#n#

目的在于，不管原回文子串的长度是奇是偶，处理后的新回文子串的长度永远为奇数，便于处理。

2.2 定义数组 `radius` 用以表示各元素的最长回文子串半径

定义数组 radius，其长度与处理后的新字符串 ns 的长度保持一致，**radius 中每个位置的值表示以 ns 对应位置的字符为中心的最长回文子串的半径，**维护结束的 radius 大概是这个样子：

ns:     # a # b # b # a # b # b #
radius: 1 2 1 2 5 2 1 6 1 2 3 2 1

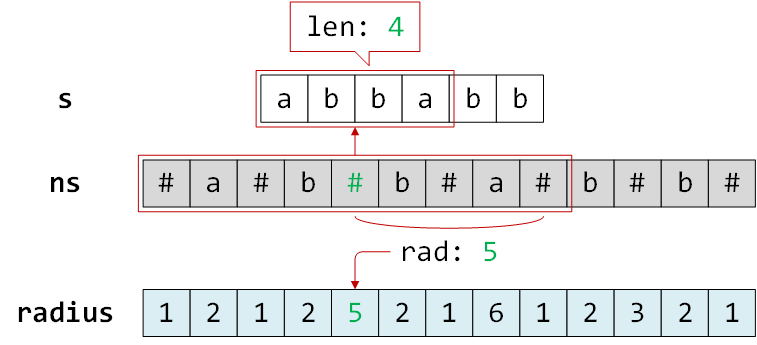
目的在于，**radius 中某个位置的值减一之后刚好等于原字符串 s 中回文子串的长度，**举个例子：下图中的 radius[4] == 5，也就是说以 ns[4] == '#' 为中心的最长回文子串 #a#b#b#a# 的半径为5，5 - 1 == 4，对应原字符串中的最长回文子串为 abba，其长度刚好是 4，符合规律且数学上也很容易证明。

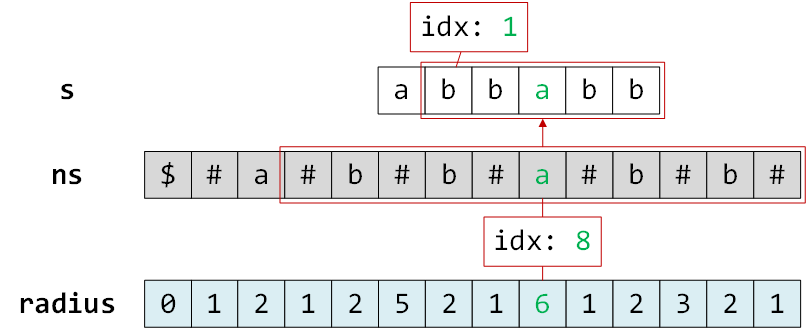
只知道长度无法确定子串，还需要知道子串的起始位置。为了便于计算，我们在新字符串 ns 开头加入字符 $，此时 radius 中某个位置的下标减去其值，再除以 2 刚好等于原字符串 s 中回文子串的起始位置，举个例子：下图中的 radius[8] == 6，也就是说以 ns[8] == 'a' 为中心的最长回文子串 #b#b#a#b#b# 的半径为 6，(8 - 6) / 2 == 1，对应原字符串中的最长回文子串为 bbabb，其起始位置刚好是 1，符合规律且数学上也很容易证明。

2.3 核心：如何维护数组 `radius`

定义四个变量，分别为：

idx 和 rad：在所有已遍历过的位置中，必然存在某个最长回文子串能够向右到达最远位置，那么这个子串的中心就是 idx，半径就是 rad。
res_idx 和 res_rad：在所有已遍历过的位置中，必然存在某个位置上的最长回文子串的长度最长，那么这个子串的中心就是 res_idx，半径就是 res_rad。

结合下面这句代码来理解具体的维护过程：

for (int i = 1; i < ns.size(); ++i)
    radius[i] = idx + rad > i ? min(radius[2*idx-i], idx+rad-i) : 1;

对于在新字符串 ns 中遍历到的下标 i，我们想知道以 i 为中心的最长回文子串的半径，从半径为 1 开始遍历自然就不能体现这个算法的精妙了，为此我们考虑以下两种情况：

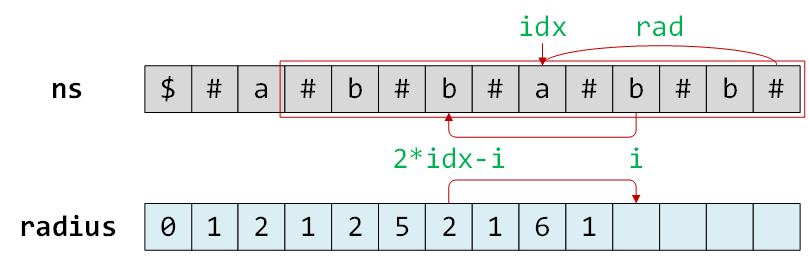
如果 idx + rad > i，说明 i 没有超出 idx 和 rad 代表的最长回文子串的范围，那么根据回文性质可以知道，在这个子串中，下标 i 的对称位置为下标 idx-(i-idx)（即 2*idx-i），而 radius 中下标 2*idx-i 的位置必然已经维护过了，也就是说以 2*idx-1 为中心的最长回文子串的半径已经知道了，那么以 i 为中心的最长回文子串的半径可以从 radius[2*idx-1] 开始遍历。
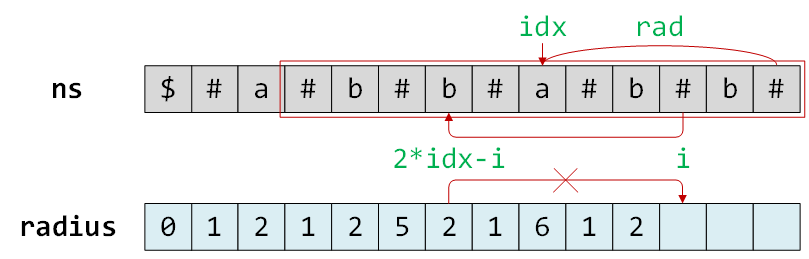
但是，对称位置 2*idx-1 的最长回文子串的半径可能超出了 idx 和 rad 代表的最长回文子串的范围，其超出部分不可能出现在 i 的右侧，但未超出部分还是可以保证满足回文要求的，那么以 i 为中心的最长回文子串的半径必须从 idx+rad-i 开始遍历。
所以，以 i 为中心的最长回文子串的半径从 min(radius[2*idx-i], idx+rad-i) 开始遍历。
如果 idx + rad <= i，说明 i 超出 idx 和 rad 代表的最长回文子串的范围，那么不存在对称位置可以参考，所以只能从半径为 1 开始遍历。

然后，维护那四个变量：

如果以 i 为中心的最长回文子串能够向右到达更远位置，则更新 idx 和 rad。
如果以 i 为中心的最长回文子串的长度更长，则更新 res_idx 和 res_rad。

最后，遍历结束，根据前文提到的两个规律从原字符串 s 中截取子串即可。

3 代码实现

class Solution {
public:
    string longestPalindrome(string s) {
        string ns = "$#";
        for (char c : s) {
            ns.push_back(c);
            ns.push_back('#');
        }
        vector<int> radius(ns.size());
        int idx = 0, rad = 0, res_idx = 0, res_rad = 0;
        for (int i = 1; i < ns.size(); ++i) {
            radius[i] = idx + rad > i ? min(radius[2*idx-i], idx+rad-i) : 1;
            while (ns[i-radius[i]] == ns[i+radius[i]]) ++radius[i];
            if (idx + rad < i + radius[i]) {
                idx = i;
                rad = radius[i];
            }
            if (res_rad < radius[i]) {
                res_idx = i;
                res_rad = radius[i];
            }
        }
        return s.substr((res_idx-res_rad)/2, res_rad-1);
    }
};

4 时间和内存对比

使用常规算法，时间和内存分别为 16 ms 和 8.6 MB。
使用马拉车算法，时间和内存分别为 4 ms 和 9.7 MB。